[Guest Post] Elliptic Curve BLS12–381 Support on Bitcoin
BLS12–381 is a newer pairing-friendly elliptic curve. Compared to curve BN-256, which was commonly used, BLS12–381 is significantly more secure and targets 128-bit security.

All other blockchains, such as Zcash and Ethereum, have to hard fork to upgrade to the new curve, since the curve used is hardcoded at protocol level. It took Zcash over a year to upgrade in Sapling. Ethereum and Tezos are still yet to upgrade after proposing it over 2.5 years ago, if they are ever going to upgrade at all.
Bitcoin can run BLS12–381 natively in the form of a smart contract without any breaking changes. This library below provides the fundament for this, making Bitcoin currently the only blockchain that supports both curves, thanks to its programmability and scalability. More curves like MNT4/6 and BW can be supported similarly, by implementing them in smart contracts.
The following is originally posted on Github by Walker, which has won the first place in the first ever Zero-Knowledge Proof hackathon on Bitcoin.
sCrypt BLS12–381 Library for Bitcoin Zero-Knowledge Proofs Smart Contract support. The current sCrypt zero-knowledge proof library is based on BN256, the BLS12–381 Library for Bitcoin is the first implementation of BLS12–381 curve pairing verification on Bitcoin. Now you can choose to use BN256 or BLS12–381 to implement zero-knowledge proof applications. Bitcoin is currently the only blockchain that supports zero-knowledge proofs and can choose multiple curves.
For platform-agnostic applications, the choice requires a tradeoff between performance (BN254) and security (BLS12–381). We recommend choosing BLS12–381 as it is more secure, still fast enough to be practical, but slower than BN254.
・ BN254 (254bit, 32byte P):

・ BLS12–381 (381bit, 48byte P):

Reference:
Table of Contents
- The curves
- Twists
- Efficient Pairing
- Coordinate systems
- Montgomery form
- Prerequisites
- How to run locally
- Library
- API
- Verifying Key and Proof data
- Test
1. Curve BLS12–381
Curve BLS12–381 is both pairing-friendly (making it efficient for digital signatures) and effective for constructing zkSnarks. The security target of BLS12–381 is 128 bits.
1.1 The curves
BLS12–381 deals with two curves,

A pairing is a bilinear map, it takes as input two points, each from a group of the same order r. these two groups call G1 and G2 .
1.2 Twists
BLS12–381 uses a twist, reduces the degree of the extension field by a factor of six. So G2 on the twisted curve can be defined over Fq2 instead of Fq12 , which is a huge saving in complexity, doing arithmetic in Fq12 is horribly complicated and inefficient.

This transforms original curve

into the curve

So these are the two groups we will be using:

1.3 Efficient Pairing
Calculation of a pairing has two parts:
- Miller loop: compute an intermediate function of the two input points f(pointG1, pointG2) recursively
- Final exponentiation: raise f to a large power c
equation 1:
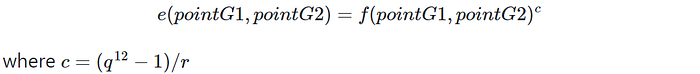
Both are quite expensive, but there’s a nice hack can reduce the impact of both of them.
1.3.1 Reduce to 3 pairings
verifying equation 2:

where α and β are known at setup, so we can precompute the second pairing e(α, β) and replace α and β with it as part of the verification key, saving one pairing.
1.3.2 One single final exponentiation
Eq.2 can be rewritten as:

e is bilinear,move the exponent (-1) into the bracket.

Plugging in Eq.1, we get:

Instead of calculating final exponentiation 4 times, which are computationally intensive, we only have to do it once in the end.
Note that, the output file of verification_key.json from snarkjs/circom, there is a vk_alphabeta_12 item precomputed, but you can't use it for precomputed f(α, β), this data is calculated by miller loop and finanl exponentiation f(α, β)^c . You can run testcase1.scrypt contract in debug mode to get precomputed f(α, β) data.
1.4 Coordinate systems
Finding the inverse of a field element is an expensive operation, so implementations of elliptic curve arithmetic try to avoid it as much as possible.
1.4.1 Affine coordinates
Affine coordinates are the traditional representation of points with just an (x, y) pair of coordinates, where x and y satisfy the curve equation. This is what we normally use when storing and transmitting points.
The basic idea is to represent the coordinate using notional fractions, reducing the number of actual division operations needed. To do this, a third coordinate is introduced and use (X, Y, Z) for the internal representation of a point.
1.4.2 Jacobian coordinates
The Jacobian point (X, Y, Z) represents the Affine point (X/Z², Y/Z³). The curve equation becomes

Note that, the easiest way to import the Affine point (x,y) is to map it to (x, y, 1).
1.5 Montgomery form
A way to calculate modulo that doesn’t require division is the so-called Montgomery multiplication. To calculate the modular multiplication operation,
- convert the multiplier into Montgomery form,
- use Montgomery multiplication,
- convert the result from Montgomery form,
2. Prerequisites
- Visual Studio Code(VSC)
- VSC Extension sCrypt IDE search sCrypt in the VSC extensions marketplace
- Node.js require version >= 12
- PC CPU >= 2.6GHz, Memory >= 24GB
3. How to run locally
- Run
npm installto install deps - Run testcase from VSCode GUI, select
testcase0.scrypttest.jsfile, right mouse button click at file edit window, select menuRun sCrypt Test
4. Library and API
4.1 Library
├─ contracts
│ ├─ bls12381.scrypt # bls12-381 library
│ ├─ bls12381pairing.scrypt # bls12-381 ZKP lib(Optimized 3-pairs)
│ └─ zksnark12381.scrypt # zk-SNARKs verifier contract example
└─ tests
└─ js
├─ testcase0.scrypttest.js # simple testcase
├─ testcaseAzksnark.scrypttest.js # testcase A
├─ testcaseBzksnark.scrypttest.js # testcase B
├─ testcaseCzksnark.scrypttest.js # testcase C
└─ testcaseDzksnark.scrypttest.js # testcase D4.2 API
static function pairCheck3Point(
PointG1 a0, PointG2 b0,
fe12 millerb1a1,
PointG1 a2, PointG2 b2,
PointG1 a3, PointG2 b3) : boolparameter(3-pairs and 1 preCompute-pair):
- a0 : A, b0 : B
- millerb1a1 : preCompute miller(α, β)
- a2 : L, b2 : ϒ
- a3 : C, b3 : δ

verifying equation 2:

4.2.1 Verifying Key and Proof data from snarkjs/Circom

You can find zkSNARK snarkjs/Circom tutorials by sCrypt.io
You need to select the bls12381 curve command line option when executing the snarkjs/Circom command, because the default is the bn128 curve. E.g,
- when compile circuit
circom ../work_circom/factor.circom --r1cs --wasm --prime bls12381 - when start a new powers of tau ceremony
snarkjs powersoftau new bls12-381 12 pot12_0000.ptau
Then you can confirm that there is a "curve": "bls12381" item in the output verification_key.json and proof.json files instead of "curve": "bn128" item.
From the proof.json file obtain the A, B, C parameters, and from the verification_key.json file obtain the α, β, ϒ, δ parameters, use the ic item and the public inputs from the public.json file to calculate the L parameter:

where public inputs w = (1, w1, …, wi)
4.2.2 verification_key.json
testcase B verification_key.json
{
"protocol": "groth16",
"curve": "bls12381",
"nPublic": 1,
"vk_alpha_1": ["32346008969010......", "760490433841......", "1"],
"vk_beta_2": [["62735191543702......", "379194604638......"],
["94606778762315......", "299061862927......"],
["1", "0"]],
"vk_gamma_2": [["3527010695874......", "305914434424......"],
["1985150602287......", "927553665492......"],
["1", "0"]],
"vk_delta_2": [["1895592553603......", "338057034563......"],
["1793381858589......", "319699776756......"],
["1", "0"]],
"vk_alphabeta_12": [
[["29062082199832......", "29798557291243......"],
["20107026956616......", "32289268603827......"],
["37794026319284......", "20272682142916......"]],
[["11743275386962......", "32259555688411......"],
["30689582621397......", "26992620205415......"],
["75601830939387......", "26615242825680......"]]],
"IC": [
["179858356000600......", "10944984983678......", "1"],
["341669953409364......", "26956794051246......", "1"]]
}4.2.3 proof.json
{
"pi_a": ["386406607244204......", "3355814159298......", "1"],
"pi_b": [["28933956745182......", "3829761206156......"],
["36211079726457......", "6620758983513......"],
["1", "0"]],
"pi_c": ["302947598381396......", "3994710045276......", "1"],
"protocol": "groth16",
"curve": "bls12381"
}4.2.4 public.json
[
"13221"
]5. Testcase
5.1 Design a circuit
Implement a circuit in the Circom language. For example, this simple proves that people know to factor the integer n into two integers without revealing the integers. The circuit has two private inputs named p and q and one public input named n.
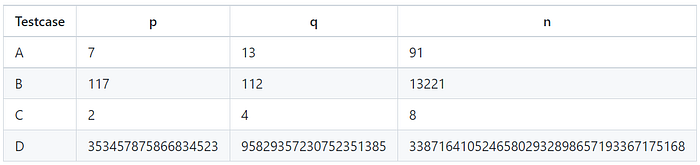
5.2 Testcase A, B, C, D
Two private inputs p and q, and one public input n.
5.3 Testnet deploy
Contract
Deploy and unlock()

Testnet — DeployTx

https://test.whatsonchain.com/tx/eba34263bbede27fd1e08a84459066fba7eb10510a3bb1d92d735c067b8309dd
